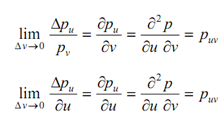Geometric Interpretation of Twist Vectors:
The twist vector at point on a surface is said to measure the twist in the surface at the point. This is the rate of change of the tangent vector Pu with respect to v or pv with respect to u, or this is the cross (mixed) derivative vector at the point. Figure illustrated the geometric interpretation of the twist vector. If we enhancement u and v by Δu and Δv respectively and draw the tangent vectors as illustrated, the incremental changes in pu and pv at point p, whose position vector is p (u, v), are attained by translating pu (u, v + Δv) and pv (u + Δu, v) to p and composing the two triangles illustrated. The incremental rate of change of the two tangent vectors becomes ΔPu/Δv and ΔPv/Δu, and the infinitesimal rate of change is specified by the following limits: