Drawback of geometrically:

The drawback of geometrically described surfaces in CAM apart from CAD is that knowing the tangent vectors to a surface enables driving a cutting tool along with the surface to machine it & knowing the normal vectors to the surface provides the correct directions for the tool to approach & retract from the surface.

In order to compute the tangent & normal vector at a point (u, v) in the given domain, we may need the partial derivatives. Imagine the parametric surface is described as follows:

p (u, v) = (x (u, v), y (u, v), z (u, v))

U_min < u  < u_max, v_min  < v < v_max

The partial derivatives w. r. t. u & v are the tangent vectors at p (u ,v) :

∂p /∂u = (∂x /∂u, ∂y/∂u, ∂z /∂u)        and    ∂p /∂u = (∂x /∂u, ∂y/∂u , ∂z /∂u )

Whereas ∂p/∂u is the tangent vector in the u-direction while ∂p/∂v is the tangent vector in the v-direction. The normal vector at p(u, v), n(u, v) is the cross-product of these partial derivatives utilizing the right-handed rule :

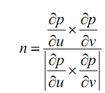
A parametric surface patch may be considered as a union of (infinite number) of curves. There are several ways to form these unions of curves; however, the simplest one is the so-called iso-parametric curve. Given a parametric surface p (u, v), if u is fixed to a value, say 0.1, and Consider v vary; this produced a curve on the surface whose u coordinate is a constant. it is the isoparametric curve in the v direction along with u = 0, 1. Likewise, fixing v to a value and considering u vary from 0 to 1, we get an isoparametric curve whose v direction is a constant. Thus, consider u be fixed at 0, 0.1, 0.1, . . . , 0.9 and 1, we will have 11 isoparametric curves p (0, v), p (0.1, v), p (0.2, v), . . . , p (0.9, v) & p (1, v). These curves sweep out the surface if we consider u change from 0 to 1 continuously. Likewise, the isoparametric curves produced by varying v cover the surface. Figure illustrated a few isoparametric curves in both of  directions.