Complementary Shear Stresses:

Consider the equilibrium of the solid element of dimensions l, b and h and acted upon through shear stress components τ_xy and τ_yx as shown in Figure. By inspection, we may recognize in which the components τ_xy on a pair of vertical planes and the pair of τ_yx on two horizontal planes satisfy independently the force equilibrium equations:

Σ F_x = 0           and     Σ F_y = 0

Now let us consider the moment equilibrium equations. τ_xy components on planes CDHG and ABFE have resultant forces Q_xy = τ_xy  . b. h that form a couple equal to (τ_xy  . b . h) × l. Similarly, the moment of the couple formed through the shear stress component τ_xy = (τ_yx . l . b) h. For equilibrium,

(τ_xy . b . h) l + (τ_yx  . l . b) h = 0

or        τ_xy = - τ_yx.

That is τ_xy is always accompanied by - τ_yx and this pair of shear stresses are known as complementary shear stresses.

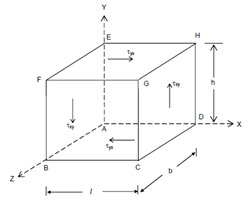
Figure

When a piece of carrot is cut within two pieces, the force exerted through the knife acts on surface parallel to the force and thus the carrot is sheared into two. As like, you might think over the several cases of load applications in our day-to-day life and identify the cases in that shear stresses are included.