Stresses and Strains

While we apply forces on solids, deformations are generated if the solid is prevented from motion (with acceleration = force/mass of solid) either partially or fully. If the solid is not restrained, it might undergo displacements without change in size or shape and these displacements are termed like rigid body displacements. If the solid is restrained tghough some other force, like reaction, which keeps the solid in equilibrium, the force shall be transmitted through the medium of the solid to the restraining support.

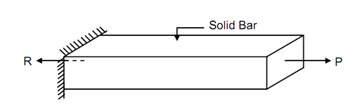
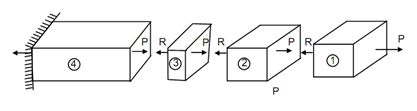
Consider the solid illustrated in Figure (a) which is pulled by the force P at the right hand side & restrained by a support at the left hand side end. If the solid is to remain in static equilibrium we know that the support must exert an equal pulling force in the direction opposite to that of force P. This restraining force, name as support reaction, is illustrated as R in Figure (a). Now let the solid being divided into a number of small bits or elements of different lengths as illustrated in Figure (b). The force P applied at the RHS end of element 1 is transmitted to the support through the medium of elements 2, 3 and 4. The similar thing is true even if you divide the solid into hundreds or even millions of elements.

(a)

                                                                                                 (B)

Now, to keep the element 1 in static equilibrium, element 2 must exert a force R (= P) on element 1. At the mean time, element 1 exerts a force P on element 2, in order that equilibrium exists at the point or surface of contact. The element 2 is again pulled by the equilibrant R exerted by element 3. Therefore equilibrium presents at each & every point or surface of contact and each element are kept in equilibrium.

The force P (or R) illustrated in the figures is just the resultant of forces applied over some area (small or even full). On any area the force might not be distributed uniformly.

Though, we might consider an infinitesimally small area ΔA over which a small part of the entire forces ΔP might be considered to be uniformly acting.

Here, the ratio dP/ dA might be called as pressure ( Compressive or sectional) at the point. Letting a small element having the area dA on one of its faces as illustrated in Figure, we understand that this pressure is accompanied by the equilibrium pressure on the opposite face of the element.

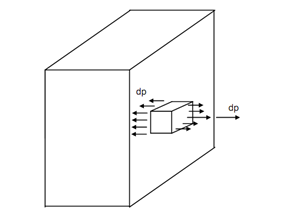
Such a set of internal pressures working on solids is said as stress. Depending on which set of planes such pressures are applied, there might be a number of such sets and they may be called stress components.

To take the easiest case, if the entire force P is uniformly distributed over the cross section A as illustrated in Figure (a), then the magnitude of stress in the solid is P/A. This entity, stress is mentioned by the symbol 'σ' and generally expressed in N/mm² units, also mentioned as Mega Pascal (MPa) as both are numerically equal.

Now let us turn our attention to deformations. The set of forces P & R are pulling the solid in opposite directions. Therefore the solid gets elongated & let this elongation be mentioned by the symbol 'δ'. If the forces be applied on the individual elements, each element shall elongate and it has been established experimentally that

 (a)  The magnitude of the individual elongations are proportional to the length of each elements, and

 (b)  The entire elongation of all the elements adds up accurately to δ.

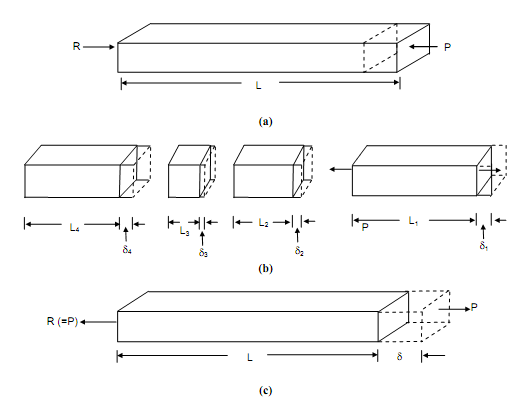
We might conclude that the ratio of elongation to length of the elements

δ₁/ L₁, δ₂/ L₂, is invariable and equal to δ/ L. This ratio is said as strain (more specifically like longitudinal strain) and mentioned by ε. If the forces applied are in the opposite direction, as illustrated in Figure (a), the solid shall get its length shortened and the deformation and strain in such a case are considered negative.