Complementary Shear Stresses

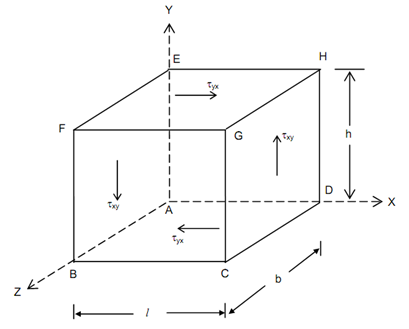
Let the equilibrium of the solid element of dimensions l, b & h and acted upon by shear stress components τ_xy and τ_yx as illustrated in Figure. By inspection, we might identify that the components τ_xy on a pair of vertical planes & the pair of τ_yx on two horizontal planes satisfy independently the force equilibrium equations:

                    Σ F_x = 0   and      Σ F_y = 0

Let us assume the moment equilibrium equations. τ_xy components on planes CDHG and ABFE have resultant forces Q_xy = τ_xy  . b. h which compose a couple equal to (τ_xy. b.h) × l. likewise, the moment of the couple formed by the shear stress component τ_xy= (τ_yx. l.b) h. For equilibrium,

 (τ_xy . b . h) l + (τ_yx  . l . b) h = 0    or  T_xy = - τ_yx.

That is τ_xy is always accompanied by - τ_yx and this pair of shear stresses are called as complementary shear stresses.

While a piece of carrot is cut into two pieces, the force exerted with the knife acts on surface parallel to the force and therefore the carrot is sheared into two. Similarly, you might think over the several cases of load applications in our day-to-day life and recognize the cases in which shear stresses are involved.