Expression for the time period:

An expression for the time period of the output waveform can be determined as follows. The equation for the capacitor charging may be written in the following general form.

                                        V_c (t ) = A + B e ^{- t /( RA + RB ) C}

 where A and B are constants which may be resolute from the following conditions.

at t = 0,              V_c (t ) =      V_cc / 3

at t = ∞ ,         V_c (t) = V_cc

Substituting in Eq. (97), we determine

                      V_cc  = A + B and V_cc  = A

from which it is found that

∴          B = 2V_cc /3

Eq. (97) now becomes

 V_c   (t) = V_cc  - (2/3) V_cc e^{- t /( RA + RB ) C}

 Now at t  = T_H, VC (t) =(2/3)V_cc ,therefore, we get

(2 /3)V cc        = V cc  - (2/3) V cc   e ^{(- tH/( RA + RB ) C)}

 (2/3) e ^{- tH/ ( RA + RB ) C}  = 1/3

e ^{tH/ ( RA + RB ) C}  = 2

from which the needed time period is given by

T_H  = (R_A  + R_B ) C ln 2

likewise, one can determine that considering the equation for discharge of the capacitor with time constant CR_B, one may find T_L as

                                                 T_L  = R_B C ln 2

The frequency of the output waveform is, thus, given by

f  =       1 / (R_A  + R_B ) C ln 2

and the duty cycle is given by

f  =  (R_A  + R_B ) (R_A  + 2R_B )

Note down that even if one selects R_A = R_B, the duty cycle may not be made 50%. However, the duty cycle may be made 50% by R_B shunting by a diode as illustrated in Figure

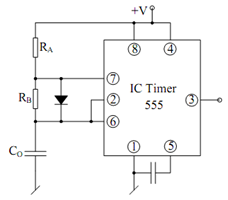
Figure: Astable Multivibrator with 50% Duty Cycle

This makes T_H = R_A C ln 2 and T_L= R_B C ln 2, so that the duty cycle is given by

                                                 δ=       R_A /R_A  + R_B

which would become 50% for R_A = R_B.