Voltage-Controlled Current Sources:

Consider the circuit illustrated in Figure (a). By judicious redrawing it may be rearranged as in Figure (b) where it is simple to recognize an NIC terminated into R realizing a -R at input port of NIC. As a result, we obtain the equivalent circuit of Figure (c). Analysis of this equivalent circuit gives

I _out    =  V_L /- R + (V_L  - V_m  ) / R = - V_m  /R

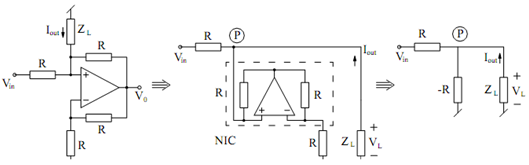
(a)                                                         (b)                                                       (c)

Figure: Realization of Voltage-controlled Current Sources

Therefore, the circuit of Figure (a) is an inverting VCCS.

A slightly different arrangement giving a non-inverting VCCS is illustrated in Figure (a).

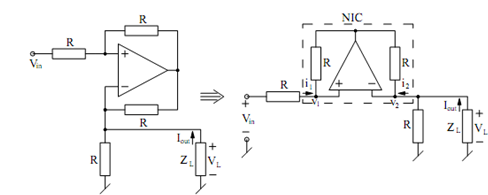
(a)                                                            (b)

Figure: A Non-inverting VCCS using an Op-amp

With some re-arrangement the circuit may be redrawn as in Figure (b) where once again, we may identify an NIC. For the NIC, we have

                                                                        V₁ = V₂  = V_L

also as the two resistors around the NIC are identical, we have  i₁ = i₂. But

i  = (V_m  - V₁ ) /R and i₂  = I_out - (V₂ /R) = i_out  - V₁/R . From these equations, it follows that

(V_m  - V₁  )/R = i_out  - V₁ /R which leads to

                                 I_out  =+ V_m /R