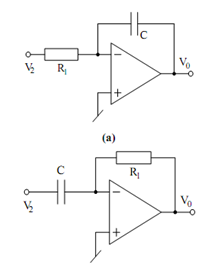
Inverting Integrator:

In Figure (a), if R_2­ is replaced by a capacitor (having transformed impedance 1/sC) one get the circuit of Figure (a) which is an inverting integrator.

(b)

Figure: (a) Inverting Integrator (Miller Integrator); and (b) Inverting Differentiator

Replacing R2 in Eq. (7.55) by 1/ sC, the transfer function of the integrator of

Figure (a) is found to be

V ₀ (S ) =- (1 / sC R ₁ ) V  (S )

or in time domain,

V₀ (t ) =-  1 /C R₁ ∫ V₂  (t ) dt

which represents an inverting integrator.