Calculate Unbalanced primary and secondary forces:

A 4-cylinder in-line engine contain crank radius of 60 mm and connecting rod length of 240 mm. The engine crank shaft rotates at 1800 rpm. The centre lines of engine are spaced at 150 mm. but the cylinders are numbered 1 to 4 from one end the cranks seem at intervals of 90^o in the end view in the order 1-4-2-3. Reciprocating mass in each of cylinder is 1.5 kg. Calculate

 (i) Unbalanced primary & secondary forces, and

 (ii) Unbalanced primary & secondary couples along reference to central plane of the engine.

Solution

The in-line cylinder centre lines are illustrated in Figure 1 along with end view.

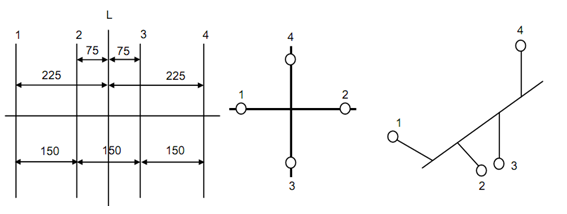
Figure

ω= (2π × 1800)/60 = 188.5 rad/s

R /g= M = 1.5 g

r = 60 mm, l = 240 mm, l/r = n = 4

Below described table is prepared to see if there is balance between the forces.

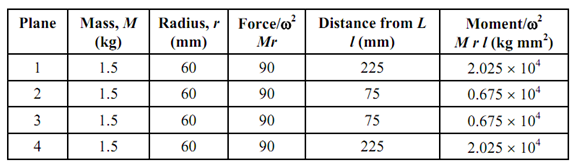
The force polygon shall be closed. We draw all of the forces toward the centre and a square is formed as in Figure 2(a).

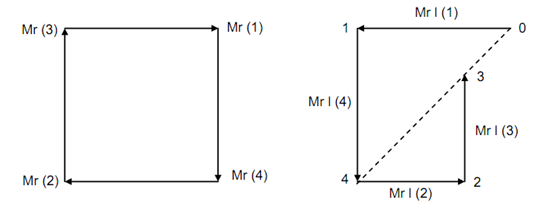
        (i) Balanced Force Polygon                                  (ii) Moment Diagram, 03 is the

           (Statically Balanced)                                       Balancing Moment                                       

The last column shows moment regarding reference plane, L. The moments of forces in planes 1 and 2 are opposite to each other and both are in horizontal plane. The moments of forces because of forces in planes 3 and 4 are opposite to each other and they are in vertical plane. The polygon is drawn along 01, 14, 42 and 23. Therefore, closing side 03 is the unbalanced moment or couple. It is in fact

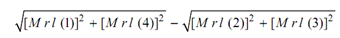
∴ Unbalanced primary moment

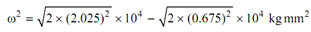
= 28638 - 9546 = 19092 kg mm2

(a)

 ∴ Unbalanced prime moment

= 19092 (188.5)²

= 678.4 × 10⁶ kg.m/s². m

= 678.4 Nm

 (b)

We have seen that the secondary force is specified by following

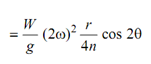
 (c)

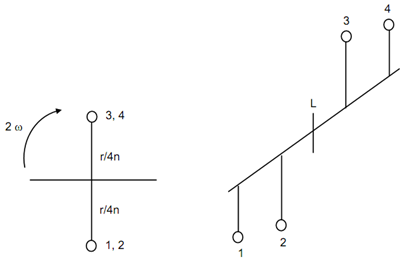
It is same as the centrifugal force of a weight W associated to crank of length   r/ 4n and revolving at a speed 2ω, that means at the speed that is twice the speed of actual crank. This explanation just supposes an imaginary secondary crank. Along inclination of θ and 2θ among actual & imaginary secondary crank 1 and 2 shall join together when 3 and 4 shall be together in the end view as illustrated in Figure 3.

The secondary forces are each equivalent as given by equation. (iii) and illustrated in Figure 3(a). Clearly they are in equilibrium. The magnitude of each of the force

 F _s = 1.5 (2 × 188.5)² ×(( 60 × 10^-3)/ 4 × 4 )  = 799.5 N          -------------- (iv)

(i)                                                     (ii)

The secondary cranks are illustrated in Figure3 (b) w. r. t. crank shaft. The reference plane L is in the centre. It might be seen from this figure that moments regarding L because of secondary forces shall add.

The unbalanced moment on shaft, M

M = 799.5 (225) + 799.5 (75) + 799.5 (225) + 799.5 (75)

= 799.5 (225 + 75 + 225 + 75)

= 799.5 × 600

= 479700 Nmm   or   478.7 Nm          -------------- (v)

Thus we see that without providing any balancing mass in a plane in a 4-cylinder engine the primary & secondary forces are balanced while moments because of both primary and secondary forces are not balanced. Generally practice secondary moments are not balanced.