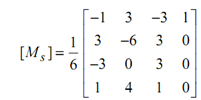Determine the equivalent bicubic formulation:

Determine the equivalent bicubic formulation of an open and closed cubic B-spline surface.

Solution

Mostly results we know may be extended to a cubic B-spline surface. Primary let us determine the matrix form of Eq. (27). This equation is identical in form to the Bezier surface equation

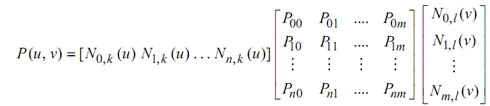
or        

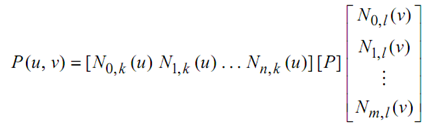
Here [P] is an (n + 1) × (m + 1) matrix of the vertices of the characteristic polyhedron of the B-spline surface patch. For 4 × 4 cubic B-spline patch, equation becomes

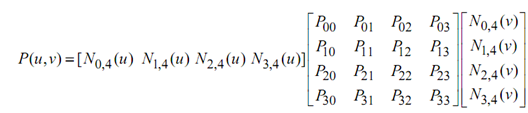
For the open patch, the B-spline functions are the similar as the Bernstein polynomials of the previous instance and the equivalent bicubic formulation results in. For, namely, a 5 × 6 open cubic B-spline patch, we obtain

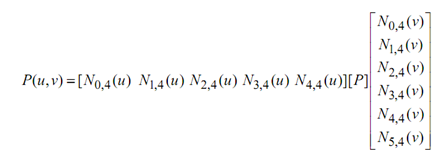
Where

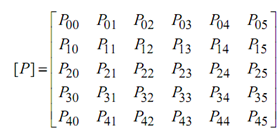
All of the the B-spline functions illustrated in this equation are calculated by following the procedure of B-spline curve. After it is done, the above equation may be decreased to

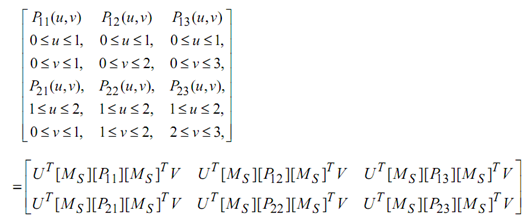
Here [P₁₁], [P₁₂], . .  . , [P₂₃] are partitions of [P]. Each of the partition is 4 × 4 and is different from its neighbour (moving into the row direction of [P]) by one row or by one column (moving into the column direction of [P]. The general form of any partition is given by

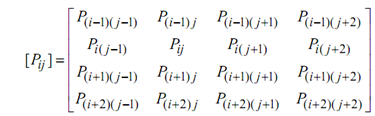
 The matrix [Ms] is the simialr as for cubic B-spline curves. It is specified by