De Boor's Algorithm:

If you know de Casteljau's algorithm for Bézier surfaces, de Boor's algorithm for B-spline surface and its modification for NURBS surfaces is only a small step away. Actually,along with the local modification property in hand, de Boor's algorithm looks extremely similar to de Casteljau's algorithm. If the equation of B-spline surface is rewritten as:

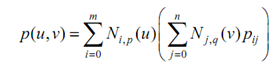
then for a fixed i, the curve in the parenthesis is just a B-spline curve indicated by the control points on row i. To make simpler our discussion, let qi (v) be indicated as follows:

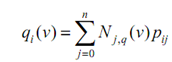
Thus, q_i (v) is a point corresponding to v on the B-spline curve indicated by the control points of row i. If v is in knot span [v_d, v_{d + 1}), then just q + 1 control points on row i are included in the computation of q_i (v), where q is the degree of N_j,q (v). These control points are p_i,d, p_{i,d - 1}, . . . , p_{i,d - q}, if v is not equal to v_d. Or else, if v is equal to v_d, a knot of multiplicity t, then the involved control points are p_{i,d - t}, p_{i,d - t - 1}, . . . , p_{i,d - q}. Thus, by using the control points from column d-q to column d-t, where t is zero if v is not a knot, we may apply de Boor's algorithm to each row to attain m + 1 new points q₀ (v), q₁ (v), . . . , q_m (v).