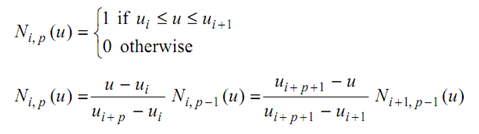Implement B-Spline Curve:

There are several ways to implement the above idea. We will look at B-Splines, that are a general form of Bezier. B-splines gives functions of the form :

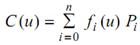
here P_i are the control points, and the {f_i (u), i = 0, . . . , n} are piecewise polynomial functions that make a basis for the vector space of all piecewise polynomial functions of some given degree and continuity at a given set of breakpoints {ui, i = 1, . . . , m}. Note  down that continuity (at least with respect to the parameter u) is dictated simply by the basic functions f_i (u) - the control points might be modified without influence the continuity. Furthermore, we would like C (u) to possess the convex hull property, along with the coordinate frame invariance property. Another property we desire our f_i (u)'s to have is that of local support - every f_i (u) is non-zero in just a (given) small number of intervals, however not over the whole domain [u₀, u_m]. As Pi is multiplied by f_i (u), moving P_i will just affect the curve shape in the range here f_i (u) is non-zero.

All of these and other gorgeous properties are possessed by B-splines. To understand B-splines, we have to first learn the B-spline basis functions. Assume U = {u₀, . . ., u_m} be a non-decreasing sequence of real numbers, i.e., u₀ î_ X₁ î_ X₂ ... î_ X_m. The u_i are known as knot points, or just knots, and U is the knot vector. After that the i-th B-spline basis function of degree-p (order p + 1), mentions N_i, p (u), is represents follow: