B-splines Functions:

We will look at B-Splines, which are a general form of Bezier. B-splines provide functions of the form are following:

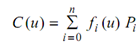
where P_i are the control points, and the {f_i (u), i = 0, . . . , n} are piecewise polynomial functions that compose a basis for the vector space of all piecewise polynomial functions of some given degree and continuity at a given set of breakpoints {u_i, i = 1, . . . , m}. Note down that continuity (at least w.r.t. the parameter u) is dictated purely by the basic functions f_i (u) - the control points may be modified without affecting the continuity. Furthermore, we would like C (u) to possess the convex hull property, in addition to the coordinate frame invariance property. Another property we desire our f_i (u)'s to have is that of local support - each f_i (u) is non-zero in just a (given) small number of intervals, but not over the overall domain [u₀, u_m]. Since P_i is multiplied by f_i (u), moving P_i shall only affect the curve shape in the range where f_i (u) is non-zero.

All of these, and other beautiful properties are possessed by B-splines. To understand B-splines, we ought to first study the B-spline basis functions. Let U = {u₀, . . ., u_m} be a non-reducing sequence of real numbers, that is, u₀ î_ X₁ î_ X₂ ... î_ X_m. The u_i are called as knot points, or simply knots, and U is the knot vector. After that the i-th B-spline basis function of degree-p (order p + 1), indicated N_{i, p} (u), is described as:

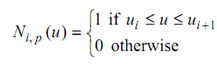
N_{i, p} (u) = (u- u_i / u_{i + p -} u_i )N_{i, p -1} (u) = (  u_{i + p +1}  - u / u_{i + p +1}  - u_{i +1} )N_{i +1}, _{p -1} (u)