Estimation and inference:

We have seen that the mathematical manipulation of economic models to arrive at a convenient estimating equation results in  the creation of an estimating equation that is autoregressive.

Autoregressive models where a lagged value of the dependent variable appears on the  right  hand  side of the equation but  the error term  is normal and  independently distributed, as obtained by  manipulation of the partial adjustment model,  can be consistently estimated by  ordinary least squares. However, the  estimators will  be biased because the lagged dependent variable is correlated with the disturbance  term.

Dynamic models where  a  lagged  value of  the  dependent variable appears on  the right  hand  side of the equation and  the disturbance term  follows an  autoregressive process,  as  obtained after  manipulation  of  the Koyck model  and the  partial adjustment model, cannot be consistently estimated by  ordinary least squares.  Let us consider- a  somewhat generalized form of  the basic model outlined  in  equations.  

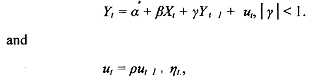
where  η,  is  distributed independent, normal  with  mean  zero  and variance σ² ,  and lρl<l.

After some manipulation we saw that the model of equations can be written as

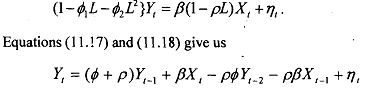
The  equation may  be  estimated by ordinary least squares  and  a  test  run  for  the coefficient of X_t-1 = 0  and the coefficient of X_t ≠ 0. This is equivalent  to a test for ρ = 0.

Various alternative. techniaues have been suggested. One serial and  easy to use technique is  that  of  instrumental variables.   Wallis propbses  the  following procedure.  Estimate equation using X_t-1 as an instrument for  Y_t-1 .  This gives

and  calculate  the  first order serial correlation  coescient = r  = ρ'.  Using  this estimate of p obtain the matrix

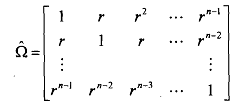
and compute the GLS (generalized least squares estimator)

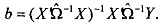
This estimator is computationally simple and consistent. Of course, asp  is unknown this is not an efficient estimator. Alternatively, one can use an  iterative, non-iinear, least squares technique to estimate the parameters of equation. To do this lag equation by  one period, multiply by p, and subtract from the original equation  to obtain

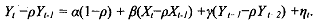
Estimation of  the above by  iterative, non-linear, least squareswill give consistent and asymptotically efficient estimators. Hypothesis testing, for significance of variables,  in these models uses standard t and F  tests as in  any other multiple regression model.