Economic theory and models with lags:

Economic theory has  several models which  lead to a similar final representation as the  two  models discussed above. The best  known of these are the  partial adjustment  and adaptive expectations models.

partial adjustment model:

The partial adjustment model  assumes that for redsons  of  ignorance, inertia, and the  high cost of change agents are unable to adjust  immeziately and fully to changes in  their  environnent.  Consider  an  example where,  Xt  denotes the  individual's disposable incomc and Y,* denotes the optimal expenditure corresponding to X,.

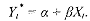
Suppose  that there  is  a  sudden  and  large  change  in  the  individual's income level. She will not  be  able  to  achieve the  corresponding  optimal  consumption level immediately because she might not know enough about her utility function to adjust to  the change at once. She may  also be  unable  to  respond  immediately because  of previous  contractual arrangements (such as an  existing apartment lease) which may constrain her immediate behavior. Therefore, her behavior may be modeled using a partial adjustment model of the form,

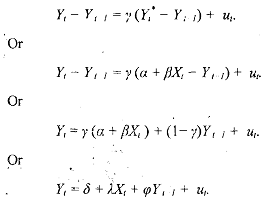
Equation assumes that consumption habits persist and consumption today is a weighted  combination of  last  period's  (Y_t-1) consumption  and  present optimal ,consumption (α + βX_i).  The speed of adjustment and the relative importance of the two different consumption  levels  in  the  final  consumption level depend on  fhe partial adjustment parameter y.  It is assumed thzt 0 <  y ≤ 1.  The closer y  is to one, the faster consumers achieve  optimal consumption  levels. Values  of  y  near zero, indicate highly persistent consumption patterns.  Substituting  yα = δ,  yβ - A,  and (1  -y)  =  β we get equation which is essentially equation, of  the lagged dependent variable model, with thc addition of an  intercept term.