Energies in hydrogen

In a hydrogen atom the energies of atomic orbitals are given by the formula:

E_n = -R/n²

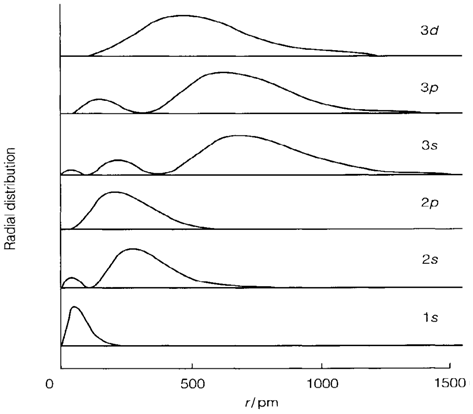
We write En to depict that the energy depends only on the principal quantum number n. Orbitals with similar n but different values of l and m have identical energy and are said to be degenerate. The energy's negative value is a reflection of the definition of energy zero, subsequent to n=∞ that is the ionization limit where an electron has sufficient energy to escape from the atom. All orbitals with finite n depict bound electrons with lower energy. The Rydberg constant R has the value 2.179×10^-18 J, but is frequently given in other units. Individual atoms' energies or molecules are frequently quoted in electron volts (eV), equal to about 1.602×10^-19 J. On the other hand, multiplying the value in joules by the Avogadro constant gives the energy per mole of atoms. In these units the

R=13.595 eV per atom

  = 1312 KJ mol^-1

The predicted energies might be compared with measured atomic line spectra where light quanta (photons) are emitted or absorbed as an electron changes its energy level, and with the ionization energy needed to remove an electron. The ionization energy is the variation between En with n=1 and ∞, and is just R, for a hydrogen atom initially in its lowest-energy ground state.