Hopfield Networks

Hopfield and Tank established a deterministic neural network model along with a symmetrically interrelated network. The equations and functions governing the behavior of Hopfield network are as:

Energy Function:

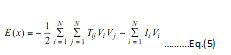
Input-Output Activation Function:

                                                     V(i) = g(u_i) =1/2(1 +tan λu_i).......Eq.(6)

Differential Motion Equation:

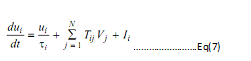
Update Equation of Neuron:

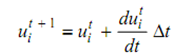                                                   ………………….Eq(8)

Here, N is the number of neurons,

V and u are output neurons and input neurons respectively

T_ij is the weighting parameter,

I is an external input neuron and

Δt is time step.

 λ and τ are gain factor and time constant with no loss of generality respectively.

In order to map a problem along with Hopfield neural network, given steps are needed as:

(a)    Option of an output representation scheme for decoding the output of a neuron in the solution of a problem.

(b)   Derivation of energy function that minimum value consequent to best solution of problem to be mapped.

(c)    Derivation of input bias currents and connectivity from the energy function.

(d)   Set up primary values for the input to the neurons that completely find out the stable output of the neurons in the network.

Steps 1, 2 and 3 play a critical role in choosing whether a problem can be resolved utilizing neural network or not. There is no direct technique for mapping constrained optimization problem upon to a neural network except for addition of terms in energy function that penalize the violation of the constraints.

Generally, three fundamental steps are adopted to accomplish the schema of resolving neural optimization problems. Primarily, construct an energy function that minimum consequent to the resolution of the problem afterward second step is to set up threshold principles for updating and judging the state of the networks to go ahead the energy function towards a minimum value. The modification of weights requires not to be taken as they are fixed. The third step is to constantly execute the comparison of the energy function values computed by the two successive iterations of updating or judging the states of the networks. The updating or judging continues until the value of the energy function is not changed several times.