Experienced users of an FMS scheduling may express conditional fuzzy propositions in the form as:

If work in queue is ◊ and processing time is◊ and distance is◊ then route selection is◊

While, appropriate states of the four linguistic variables are placed into the empty boxes for each exacting proposition. Because the variables of work in queue, processing time, and distance contain three states each, the sum of possible ordered pairs of these states is twenty-seven. For all of these ordered pairs of states, we have to calculate an appropriate state of variable Route selection. A convenient method of defining all needed rules is a decision Table that is identified also as a fuzzy association memory or FAM bank matrix. It consists of 27 (3 *3 *3) rules and is constructed for Route selection as displayed in Table no.6.

The route selection criteria now utilized to derive fuzzy inference rules are displayed as an illustration as:

1.      IF (Work_in_queue is SW) and (Processing_time is SP) and (Distance is ST) THEN (Route_selection is MX)

2.      If (Work_in_queue is SW) and (Processing_time is SP) and (Distance is MT) then (Route_selection is MX)

:

:

     27. If (Work_in_queue is LW) and (Processing_time is LP) and (Distance is LT) then (Route_selection is MN)

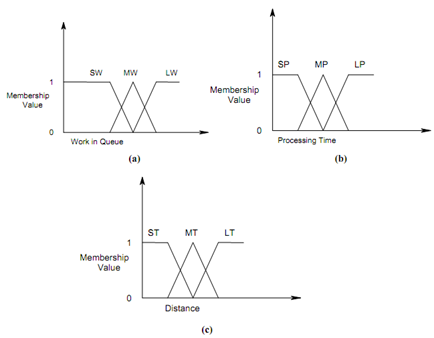
Figure: Membership Functions of Fuzzy Set Variable, (a) Work in Queue; (b) Processing Time; and (c) Distance

                       Table no.6 of: Inference Rules for Rout Selection using Three Inputs and One Output