Application to Truss Problems:

In this section, we will apply Castigliano's theorem to calculate the deflections in a truss.

Let a truss within m members be subjected to a system of loads P₁, P₂, . . . , etc. The forces in the members of the truss might be obtained by standard methods. Assume F_i be the force in the i^th member because of the above system of forces. Let L_i & A_i be respectively the length & area of cross-section of the member. After that the strain energy stored in this member shall be

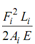
where E is the Young's modulus of the material.

Then, the total strain energy stored in the truss might be written as follows :

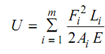
Now, as per Castigliano's theorem the deflection δ_n under the load P_n in its direction shall be

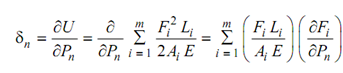
Let us observe this equation closely.

∂F_i /∂P_n is the rate at which F varies along with P with all other loads remaining constant or in other terms it is the force in the member while a unit load is applied rather then P_n, while all of other loads are zero.

The above concept may still be applied to discover the deflection in any direction at any joint of the truss even while no load is working in that direction or at that point. In this case, we introduce a fictitious force Q at the pint in the direction in which we need the deflection. After that we determine the member forces for the load system that now includes Q also.

Then,

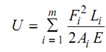        (now F_i includes the effect of Q also)

Therefore,

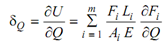
However, in real problem there is no Q or its value is zero. Thus we put Q = 0 in the above expression and get δQ.

The concept of unit load might be brought in even here. Now while we include Q in the load system F_i may be written as

F_i  = F_iP  + F_iQ  (principle of superposition)

where F_iP & F_iQ are the member forces only because of the P_s and Q, respectively.

Then,

U  =∑ (F_iP  + F_iQ )²  Li/2 Ai Ei

And

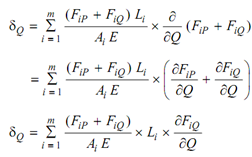
 (As F_iP does not involve Q and, hence,   ∂F _iP /∂Q = 0 ).

While we put Q = 0 in the above expression it decrease to

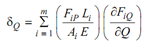
∂F_iQ /∂Q is nothing but the member force because of a unit load in the direction of Q at the point of application of Q while all other loads are zero.