Freudenstein's Equation for Slider Crank Chain for Three Accuracy Points:

In slider crank mechanism, the displacement of the slider 'B' needs to be coordinated along the rotation of crank O₂ A. The mechanism is illustrated in Figure. Since in case of four bar chain, if the displacement of the slider is supposed proportional to the crank rotation, it may be expressed as:

                                                    l₁ - l_1i  = C (θ - θ_i )

For an interval θ_i ≤ θ ≤ θ_f

 l₁ f   - l_1i  = C (θ _f - θ_i )

 Here   C = constant of proportionality,

l₁ = distance of slider from origin, and

θ = angle of rotation of crank from the line of stroke.

 Subscript 'i' refers to the primary value and 'f' to final value.

There are five design parameters that are θ, l₁, l₂, l₃ and l. For three accuracy points the three parameters l₂, l₃ and are find out. The coordinates of points A & B are (l₂ cos θ, l₂ sin θ) and (l₁, l), respectively.

The distance

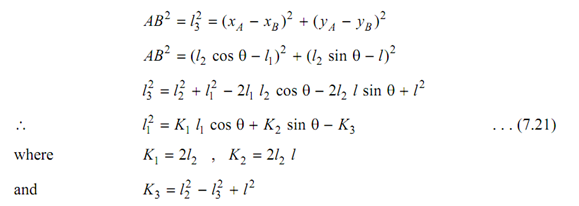
Eq. (7.21) is the Freudenstein's equation for slider crank chain. The given steps are followed to find lengths:

(a) Achieved three accuracy points using Chebysher's spacing, that is  θ1, θ2 and θ3.

(b) Achieved corresponding values of l₁₁, l₁₂ & l₁₃.

(c) Achieved three equations in K₁, K₂ & K₃.

(d) Achieved l₂, l₃ and l from values of K₁, K₂ & K₃.