Freudenstein's Equation for Four Bar Chain for Three Accuracy Points:

There are seven design parameters. There are θ, φ, rx, ry & three ratios of link lengths. In the current section we will consider three accuracy points. The parameters symbol θ, φ, r_x, & r_y are either specified or supposed and the three length ratios l₁ /l₂, l₁/l₃ and l₁/l₄ are to be estimated as design parameters.

In reference to Figure, the coordinates of the point A are (l₂ cos θ, l₂ sin θ) and for point B are

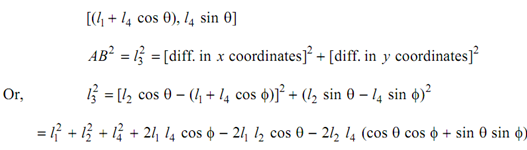
Dividing this expression through 2l₂ l₄ and after rearranging the following equation is achieved :

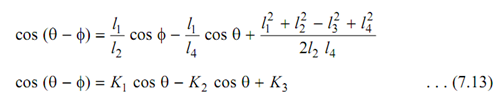
here

The given steps are followed to determine length ratios :

 (a) Achieved three accuracy points using Chebyshev's spacing, that means x₁, x₂ and x₃ from Eq. (7.10).

 (b) Achieved the corresponding values of y₁, y₂ & y₃ using given function y = f (x).

(c) Using Eqs. (7.11) & (7.12), determine (θ₁, θ₂ and θ₃) and (φ₁, φ₂, and φ₃) equivalent to values of x & y.

 (d) Attain three equations in K₁, K₂ and K₃ by putting the three related pairs of the angles (θ₁ & φ₁), (θ₂ & φ₂), and (θ₃ & φ₃).

 (e) Solve out these three equations for K₁, K₂ & K₃.

 (f) Find out length ratios from values of K₁, K₂ & K₃.

 (g) Suppose one link length or it can be given. Find out other lengths that can be find out from the length ratios. The lengths l₁ & l₃ will always be positive. The negative values of l2 or l4 may be interpreted in the vector sense. The negative sense shall signify that their layouts are opposite to the fixed link.