Chebyshev's Spacing of Accuracy Points:

Assume xi and x_f be initial and last values of variable x respectively. The function E_f (x) is required to be generated in the interval x_i = x_f. Consider the generated function be F = ( x, R₁ , R₂  ... R_k ) where R₁, R₂ . . . R_k be design parameters. The difference E (x) among the desired function & generated function may be represented by

                        E ( x) = f (x) - F ( x, R₁ , R₂  . . . R_k )                                                 . . . (7.11)

 At precision points or accuracy points say for x = x₁, x₂ . . . x_k desired and generated functions agree and E (x) shall be zero. At other points E (x) shall have some value and that shall be the error. E (x) is known as 'structural error'. It is wanted that E (x) must be minimum and thus, spacing of accuracy points is very significant. An exact analysis for E (x) to be minimum is very complicated. The Chebyshev's spacing of accuracy points may always be taken as a primary approximation. The accuracy points as said by Chebyshev's spacing are given following

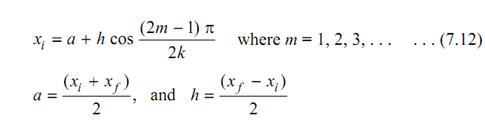
Furthermore Chebyshev's accuracy points attained from Eq. (7.12) will be utilized. The accuracy points may also be attained by the graphical method also as described in the following steps:

(a) Draw a circle of radius 'h' & centre on the x-axis at a distance 'a' from O.

 (b) write regular polygon of side '2k' in this circle such as the two sides are perpendicular to the x-axis.

 (c) Find out the locations of 'k' accuracy points by projecting the vertices on x-axis as illustrated in Figure

Figures (a) and (b) illustrate the geometric method for k = 3 and 4, respectively. As the aim is to acquire the values of accuracy points, semi-circles presenting inscribed polygons are adequate.