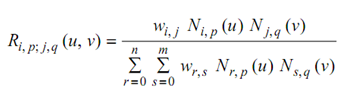Geometric characteristics:

The NURBS curve shall exhibit the following geometric characteristics:

-          Bezier & non-rational b-spline curves are special cases.

 -         Local Approximation : If a control point is moved or a weight is altered, it shall influence the curve only in p = 1 knot spans.

-          Strong Convex Hull Property: If u ∉ [u_i , u_{i +1} ] , then C (u) lies in the convex bull of P_{i - p}, . . . , P_i.

-          Invariance under affine & perspective transformations.

-          The similar differentiability property as with the basic functions.

-          If a specific weight is set to zero, then the equivalent control point has no influence at all on the curve.

If         w_i → + ∞,

then

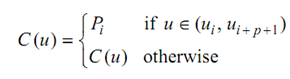
NURBS surfaces might be analyzed similarly utilizing the bivariate rational basis functions