Method of Relative Velocity and Acceleration:

For this reason, a link of a general shape might be considered to begin with. It is illustrated in given fig. Assume there is any arbitrary two points A & B moving with velocities V_A & V_B. The velocity of B relative to A might be represented by V_BA. Assume relative velocity V_BA makes an angle θ along line joining A & B. V_BA might be resolved into two components V_BA cos θ along AB & V_BA sin θ perpendicular to AB. As the link is rigid, distance AB remains constant. Thus, component of velocity of B relative to A along AB might not exist. Thus,

V_BA  cos θ = 0 or cos θ = 0

Or θ= π/2

It means a rigid link contain rotation relative to point A, plus translation along velocity of A.

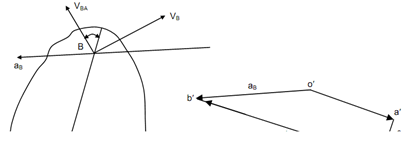
Thus, the direction of V_BA is perpendicular to the line joining A & B. If V_A is known in magnitude & direction and for V_B just direction is known, the magnitude may be finding out by drawing a polygon as stated following:

 (1) First the velocity of A that means V_A is plotted through supposing an appropriate scale from an arbitrary chosen point o which represents fixed reference. Consider it be represented by 'oa'.

(2) Now, draw a line by o parallel to the direction of velocity of B, that VB.

(3) After that, draw a line through point 'a' that is parallel to the perpendicular to the line AB that meets the direction of V_B at point 'b'.

In this velocity polygon oab, 'ob' represents velocity V_B in magnitude & direction. After drawing velocity polygon, we may proceed for finding of magnitude of acceleration of point B. If direction of the acceleration of B is known and acceleration of point A is known in magnitude & direction. The vector equation may be written as:

                                                            a_B  = a _A  + a_BA

As

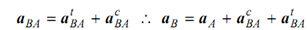
Here a_BA is acceleration of B relative to A; at is tangential component of a_BA and  is centripetal component of a_BA.

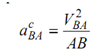
This is directed from B to A along AB while at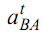 contain direction perpendicular to AB.

Acceleration polygon may be drawn as:

 (1) In magnitude and direction, plot acceleration of A by supposing suitable scale. a_A is represented by o′a′.

 (2) Plot centripetal component 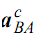by drawing line parallel to AB and shows its magnitude according to the vector equation. 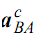is showed by a′a′₁.

 (3) From a₁ draw a line perpendicular to aa₁′ or parallel to the perpendicular to AB to show direction of .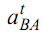

 (4) Draw a line parallel to the direction of acceleration of B that means a_B from fixed reference o′ to meet the line signifying direction of 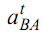. They meet at the point b′. o′b′ signify acceleration of B in direction & magnitude.