Klein's Construction for Determining Velocity And Acceleration Of Slider Crank Mechanism:

There are some special techniques for finding velocity & acceleration of slider in slider crank chain.

Case I

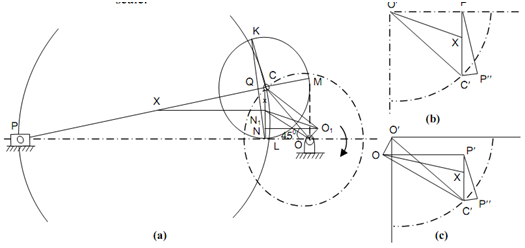
In this case, crank rotation is supposed uniform. The configuration diagram of slider crank chain is illustrated in Figure (a). The method is shown in following steps:

(a) Draw configuration diagram at an appropriate scale.

(b) Extend PC if essential to meet perpendicular to stroke line at M.

(c) Draw a circle with C like centre and CM like radius.

(d) Draw another circle along CP as diameter.

(e) Draw common chord KL of these two circles & extend if essential to meet line of stroke at N. OCQN is acceleration polygon.

(f) NO provides acceleration of piston at a scale equivalent to ω² × configuration scale.

Proof

In the acceleration polygon OCQN    

OC → Centripetal acceleration of C,

CQ → Centripetal acceleration of P associated to C,

QN → Tangential component of acceleration, and

NO → Acceleration of piston.

Connect K with P & C. The triangle CKP & CQK are same

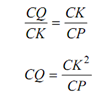
But CK = CM

Hence,

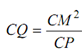
The acceleration according to the methods described earlier has been drawn in Figure (b). The acceleration polygon o′ c′ p″ p′ appears to be likewise to OCQN. If ω is angular velocity of crank, VC = OC ω and likewise velocity of piston VP = ω OM.

 Also,                          V_PC   = ω CM

Thus, it shows that CQ represents centripetal acceleration 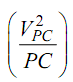to the scale ω² × configuration scale. Hence, these two polygons are likewise and ON define acceleration of the piston to the above indicated scale. For a point X on the linking rod, draw a line by X parallel to the line of stroke to intersect CN at x & acceleration of x is illustrated by 'ox'.

Case II

In this case, crank rotates & contains angular acceleration. The acceleration polygon is reproduced in Figure (c). The point Q is finding out in the similar way like in Case I. From O, draw a line perpendicular to CO and plot tangential acceleration OO₁. Join C with O₁. Through O₁, draw a line parallel to line of stroke to meet KL & N₁. The acceleration polygon is O₁ C Q N₁ & O₁ N₁ is acceleration of the piston. For a point X on CP join x (determined in Case I) with O₁. This acceleration polygon is likewise to Figure (c).