General Method for Velocity and Acceleration:

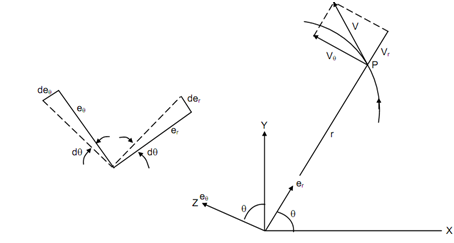
We begin with plane curvilinear motion utilizing polar coordinates to mention the position vector 'r' and its angular coordinate 'θ' calculated from a fixed reference axis as illustrated in .Assume e_r & e_θ unit vectors in radial & transverse directions respectively.

These unit vectors contain positive directions in increasing r and θ. The vectors e_r and e_θ are parallel to the positive senses of V_r & V_θ. Both of these unit vectors shall swing by the angle in the time dt. As illustrated in figure, their tips move by the distances | d e_r = 1| = 1 × dθ = dθ in the direction of e_θ, and by de_θ = 1 × d θ = d θ in the direction opposite to that of e_r. Hence,

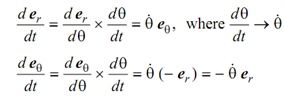
The velocity of a particle P which contain position vector 'r' is given by following

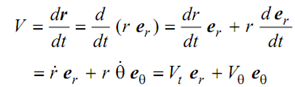
here V_r & V_θ are the components of velocity in radial direction & transverse direction. The acceleration of particle P is given by following

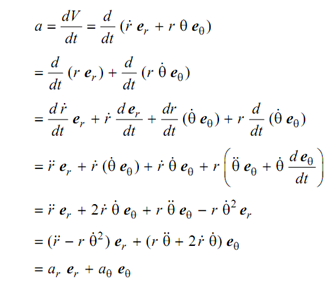
here a_r represents radial component and a_θ represents transverse component of acceleration.

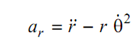
                And

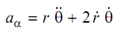
Here,

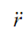→ Acceleration of slider along with slotted link,

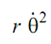  → Centripetal acceleration,

→ Tangential component of acceleration, and

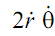→ Coriolis' component of acceleration.