Determining Coriolis Component of Acceleration:

In rigid body rotation, distance of any point from the axis of rotation remains fixed. If a link rotates around a fixed centre and, at the similar time, a point moves over it along the link, the absolute acceleration of the point is illustrated by the vector sum of

(1) The absolute acceleration of the coincident point relative to that the point, under consideration, is moving;

(2) Acceleration of the point associated to the coincident point; and

(3) Coriolis' component of acceleration.

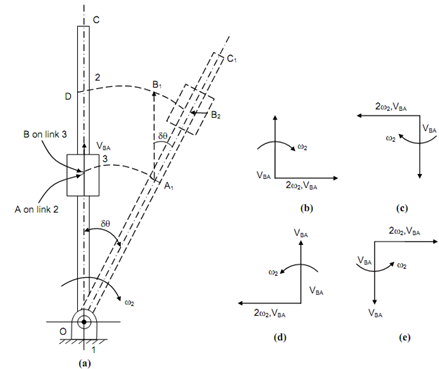
Figure illustrates a link 2 rotating at constant angular speed say ω₂, this move from position OC to OC₁. Throughout this interval of time, the slider link 3 moves outwards from position B to B₂ along constant velocity V_BA (A is point on link 2 shich coincides along B that is on link 3). The motion of the slider 3 from B to B₂ might be considered in the three stages which are following:

(a) B to A₁ because of rotation of link 2,

(b) A₁ to B₁ because of outward velocity V_BA,

(c) B₁ to B₂ because of acceleration perpendicular to the link which is the Coriolis' component of acceleration.

Arc B₁ B₂ = Arc DB₂ - Arc DB₁

= Arc DB₂ - Arc AA₁

Also

Arc B₁  B₂  = A₁  B₁  δ θ = V_BA  δ t ω₂ δ t

                                         = V_BA ω₂ (δt) ²

The tangential component of the velocity is perpendicular to the link is say V_t and this is given by following

                        V_t = r ω

In this case ω has been supposed constant and slider moves having constant velocity. Thus, tangential velocity of point B on the slider 3 shall result in uniform increase in tangential velocity due to uniform increase in value of r in the above equation.

To result in consistent increase in value of V_t, there need to exist constant acceleration perpendicular to link 2.

Hence,

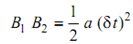
here a is the acceleration.     

 ∴         1/2 a (δt )² = V_BA ω₂ (δt)²

                           a = 2 V_BA  ω₂

It is Coriolis' component of acceleration and will be mentioned by.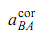

Hence ,

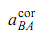             = 2 ω₂ V_BA

 The directional relationship of V_BA and 2 ω₂ V_BA is illustrated in Figures (b), (c), (d) and (e). If slider moves to centre of rotation o, its velocity may be transmitted to other side so that this is directed outwards.

The direction of Coriolis' component of acceleration is illustrated by the direction of the relative velocity vector for the two coincident points rotated by 90^o in the direction of the angular velocity of the rotation of the link.

If the angular velocity ω₂ & the velocity V_BA are differ, they will not influenced the expression of the Coriolis' component of acceleration however their instant values will be utilized in determining the magnitude and this value shall be applicable at that instant.