Find accuracy of ammeter:

Example: An ammeter, along with a 10 mA full scale deflection and aninternal resistance of 400 ? is placed within a circuit along with a 20 V power source and a 2 K? resistor show in below figure.

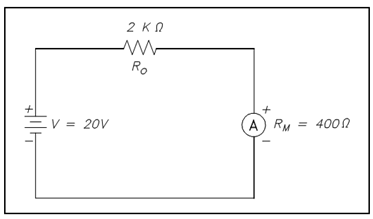
Figure: Ammeter Accuracy

Find: 1. accuracy

2. %loading error

3. true current

4. measured current

1. K_A= R/R_o + R_m

K_A= 2000/2000 + 400

K_A = 0.833 or 83.3%

2. % loading error = (1- K_A) (100%)

% loading error= (1- 0.833)(100%)

% loading error=16.7%

3. I_o =V/ R_o

= 20/2000

I_o = 0.01A or 10mA

4. I_w=V/R_o+ R_m

= 20/2000 + 400

I_w =8.33x10^-3A or 8.33mA

An ammeter within a full scale I_m could be shunted along with a resistor R_SH in sequence to measure current in excess of I_m. A reason for shunting an ammeter is to extend the range of the ammeter and, by, measure currents higher than the original full scale value.

Through Kirchhoff's current law,

I_SH = I_T - I_m

Because the voltage across the shunt has to be equivalent to the voltage across the ammeter; shunt resistance is calculated as given below:

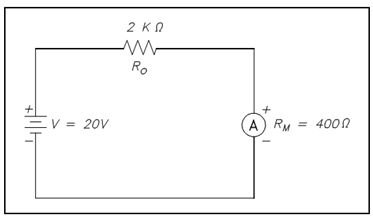
Figure: Ammeter with Shunt

I_SHR_SH = I_mR_m

R_SH = I_mR_m/I_SH

R_SH = I_mR_m/I_T - I_m

Thus, the input resistance of a shunted ammeter is associated to the meter and shunt resistance. Given Equation (14-8) is a mathematical representation of this relationship.

NOTE: Whenever computing accuracy for a shunted ammeter, use R ¹_m within place of R_m.

R ¹_m = R_mR_SH /R_m + R_SH                                                                  (14-8)

Equation (14-9) is a mathematical representation of the relationship among input voltage and current to the ammeter and the value of input resistance.

R ¹_m =V_in/I_in + I_mR_m/I_T                                                                    (14-9)