Vector Representation of Impedance:
Any impedance Z can be denoted by a complex number R + jX, here R can be any non-negative real number and X can be any real number. These numbers can be plotted as points in the RX half-plane or as vectors with their end points at the origin (0 + j0). These vectors are termed as impedance vectors.
Assume how an impedance vector changes as either R or X or both are differed. When X stays constant, a raise in R causes the vector to get longer. When R stays constant and XL gets larger, the vectors also grow longer. When R remains similar as XC gets larger (i.e., negatively), the vector grows longer again. Think of point symbolizing R + jX moving around in the plane, and visualize where the corresponding points on the resistance and reactance axes lie. Such points can be found by drawing straight lines from the point R + jX to the R & X axes therefore the lines intersect the axes at right angles. This is as shown in figure below for numerous various points.
Now think of the points for R & X moving toward the right and left or up and down on their axes. Assume what occurs to the point R+ jX and the corresponding vector from 0 + j0 to R + jX in different scenarios. This is how impedance changes as the resistance and reactance in a circuit are diverse.
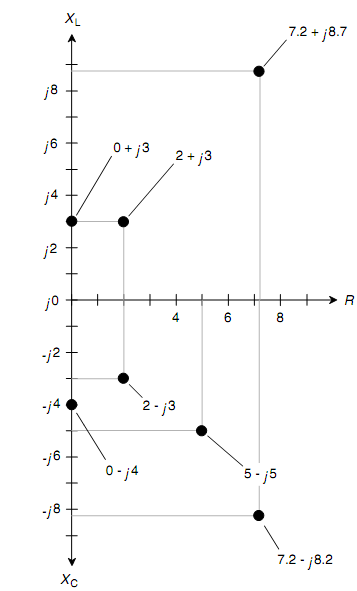
Figure: The RX impedance half-plane showing few points for particular complex-number impedances.