Sine Waves As Circular Motion:

Assume that you dangle a glowing ball around and around at the end of a string at a rate of one revolution per second. The ball therefore explains a circle in space (as shown in figure a). Visualize that you swing the ball around so that it is always at similar level; it takes a path which lies in a horizontal plane. Imagine that you perform this in a pitch-dark gymnasium. When a friend stands some distance away with her or his eyes in the plane of the ball's path, what your friend see? Only the glowing ball, oscillating back and so. The ball looks to move toward the right, slow down, and then oppose its direction, going back toward the left (as shown in figure b). Then it moves faster and faster and then again slower down, reaching its left-most point, at which it turns about again. This goes on and on, with a frequency of 1 Hz, or a complete cycle per second, since you are swinging the ball around at one revolution per second.

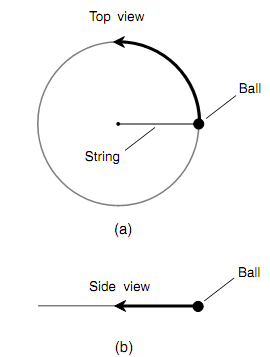
Figure: Swinging ball and string. (a) as seen from above; (b) as seen from some distance away in the plane of the ball's circular path.

When you graph the position of the ball as seen by your friend with respect to time, the outcome will be a sine wave (as shown in figure below). This wave has similar characteristic shape as all sine waves. The standard, or basic, sine wave is explained by the mathematical function y = sin x in the (x, y) coordinate plane. The common form is y = a sin bx, here a and b are real-number constants.

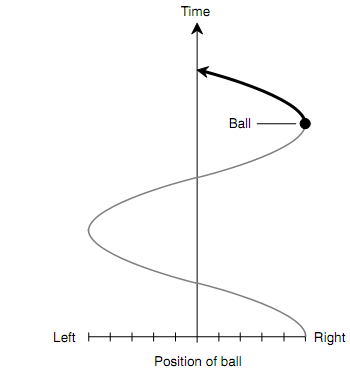
Figure: Position of ball as seen edge-on as a function of time.