Sawtooth Waves:

Some of the ac waves oppose their polarity at constant though not instant rates. The slope of the amplitude-versus-time line specifies how fast the magnitude is changing. These waves are known as sawtooth waves since of their appearance.

In the figure below, one form of sawtooth wave is shown. The positive-going slope (rise) is tremendously steep, as with a square wave, but the negative- going slope (fall or decay) is steady. The period of the wave is the time among points at identical positions on two consecutive pulses.

The other form of sawtooth wave is just the opposite, with a steady positive-going slope and a vertical negative-going transition. This kind of wave is sometimes termed as a ramp (figure shown below). This waveform is used for scanning in cathode-ray-tube (CRT) television sets and oscilloscopes.

Sawtooth waves can have increase and decay slopes in an unlimited number of various combinations. One illustration is shown in figure below. In this situation, the positive-going slope is similar as the negative-going slope. This is a triangular wave.

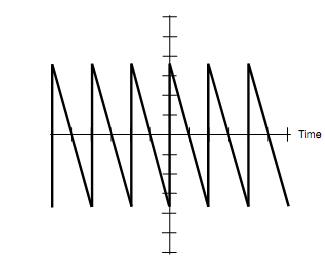
Figure: A fast-rise, slow-decay sawtooth wave.

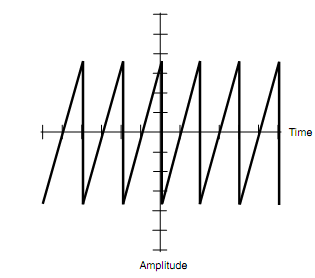
Figure: A slow-rise, fast-decay sawtooth wave, also termed as ramp wave.

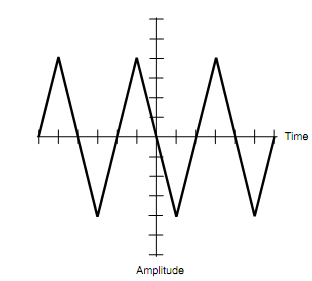
Figure: A triangular wave.

PROBLEM:

Assume that each horizontal division in figure below symbolizes 1.0 microsecond (1.0 µs or 1.0 x 10^-6 s). Compute the period of this triangular wave? Determine the frequency?

SOLUTION:

The simplest way to look at this is to compute the wave from a point where it crosses the time axis going upward and then find the next point (to the left or right) where the wave crosses the time axis going upward. This is four horizontal divisions, at least inside the limit of our capability to tell by looking at it. The period T is thus 4.0 µs or 4.0 x 10^-6 s. The frequency is the reciprocal of this:

f = 1/T = 1/(4.0 x 10^-6) = 2.5 x 10⁵ Hz.