Points In The Rl Quarter-Plane:
In a circuit having both resistance and inductance, the characteristics become 2-dimensional. You can familiarize the resistance and reactance half-lines perpendicular to each other to build a quarter-plane coordinate system, as shown in figure below. The Resistance is shown on the horizontal axis, and the inductive reactance is plotted vertically, leaving upward.
Each and every point on the RL quarter-plane corresponds to exclusive complex number impedance. On contrary, each complex-number impedance value corresponds to an exclusive point on the quarter-plane. The impedances on RL quarter-plane are written in the form of R + jXL, here R is the resistance in ohms, XL is the inductive reactance in ohms, & j is the unit imaginary number, that is, the positive square root of -1. The value j in this application is termed as the j operator.
Assume that you have a pure resistance, let say, R = 5 ohms. Then the complex-number impedance is 5 + j0 and at the point (5, 0) on the RL quarter-plane. When you have a pure inductive reactance, like XL = 3 ohms, then the complex-number impedance is 0 + j3 and is at the point (0, 3) on the RL quarter-plane. Such points, and a few others, are shown in figure below.
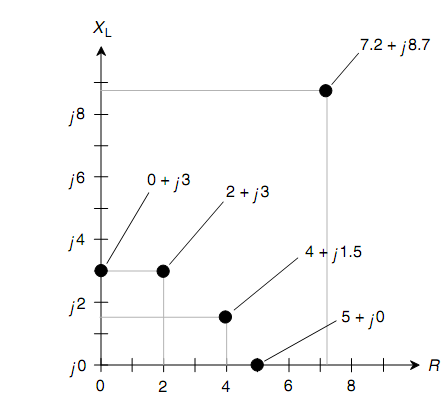
Figure: The RL impedance quarter-plane showing five points for specific complex-number impedances.
In the real world, all the coil inductors have several resistances since no wire is a perfect conductor. All resistors have at least a little bit of inductive reactance since they have wire leads at each end and they have a measurable physical length. There is no such thing as the mathematically perfect pure resistance such as 5 + j0 or a mathematically perfect pure reactance such as 0 + j3. At times you acquire get close to like ideals, though absolutely pure resistances or reactances never exist (apart from seldom in quiz and test problems, obviously!).
In electronic circuits, resistance and inductive reactance are at times both incorporated deliberately. Then you get impedances values like 2 + j3 or 4+ j1.5.
Recall that the values for XL are reactances (stated in ohms) and not inductances that are stated in henrys). Reactances differ with the frequency in an RL circuit. Changing the frequency has the result of making the points move in the RL quarter-plane. They shift vertically, going upward as the ac frequency rises and reduces as the ac frequency reduces. When the ac frequency goes down to zero, thus resultant in dc, the inductive reactance vanishes. Then XL = 0, and the point is along the resistance axis of the RL quarter-plane.