Inductors In Parallel:

When there is no mutual inductance between two or more parallel-connected inductors, their values add up such as the values of resistors in parallel. Assume that you have inductances L1, L2, L3,..., Ln associated in parallel (as shown in figure below). Then you can find the reciprocal of the total inductance 1/L by using the following formula as follows:

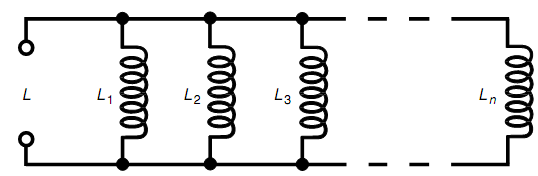
Figure:  Inductances in parallel add like resistances in parallel.

1/L = 1/L₁ + 1/L₂ + 1/L₃ + ....+ 1/L_n

The total inductance L is establishing by taking the reciprocal of the number you obtain for 1/L. Which is:

L = 1/ (1/L₁ + 1/L₂ + 1/L₃+  ...+ 1/L_n)

   = (1/L₁ + 1/L₂ + 1/L₃ + ...+ 1/L_n)^-1

Again, as with the inductances in series, it is significant to recall all the units have to concur. Do not mix microhenrys with millihenrys or henrys with nanohenrys. The units you use for the separate component values will be the units you obtain for the final result.

Let us not concern ourselves with what occurs whenever there is mutual inductance. At times mutual inductance raises the total inductance of a combination to values greater than the formulas point to, and in other situation mutual inductance decreases the net inductance of a combination. Engineers at times should worry about mutual inductance whenever building radios or other sophisticated electronic circuits, mainly at high frequencies.

PROBLEM:

Assume that there are three inductors in series with no mutual inductance. Their values are 1.50 mH, 150µH, and 120 µH. What is the total inductance of the combination?

SOLUTION:

Transform all the inductances to the similar units and then add them up. Let us use millihenrys (mH). The second and third values must be multiplied by 0.001 (10^-3) to transform from microhenrys to millihenrys. Therefore, the total series inductance Ls is as follows:

L_s = (1.50 + 0.150 + 0.120) mH = 1.77 mH