Capacitors In Parallel:

The Capacitances in parallel add just like resistances or inductances in series as shown in figure below. That is, the total capacitance is the sum of the separate component values. Again, you require to be sure that you use similar size units all the way through.

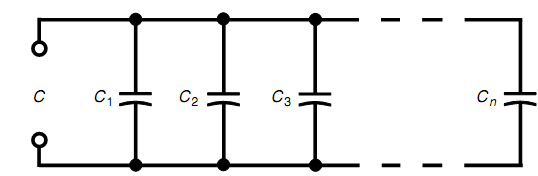
Figure: Capacitances in parallel add just like resistances or inductances in series.

PROBLEM:

Three capacitors are put up in parallel, containing values of C1 = 0.100 µF, C2 = 0.0100 µF, and C3 = 0.00100 µF. Determine C, the total capacitance?

SOLUTION:

Add them up: C = 0.100 µF +            0.0100 µF + µF 0.00100 = 0.11100 µF.

Since the values are given to three significant figures, the final result must be stated as C = 0.111 µF.