Absolute-Value Impedance:

At times you will study or hear that the "impedance" of some device or component is a certain number of ohms. For illustration, in audio electronics, there are "8-ohm" speakers & "600-ohm" amplifier inputs. How can producers quote a single number for a quantity which is 2-dimensional and requires two numbers to be totally expressed? There are two answers to this.

At first, figures like this commonly refer to devices which have purely resistive impedances. Therefore the "8-ohm" speaker actually has a complex-number impedance of 8 + j0, and the "600-ohm" input circuit is designed to operate with complex-number impedance at or near 600 + j0. Secondly, engineers at times talk about the length of the impedance vector, calling this an assured number of "ohms." When you talk about "impedance" in this manner, then theoretically you are being ambiguous since you can have an infinite number of various vectors of a given length in the RX half-plane.

The expression "Z = 8 ohms," when no particular complex impedance is provided, can refer to the complex vectors 8 + j0, 0 + j8, 0 - j8, and any vector in the RX half-plane whose length is 8 units. This is shown in figure below. There can exists an infinite number of various complex impedances with Z = 8 ohms in a purely technical logic.

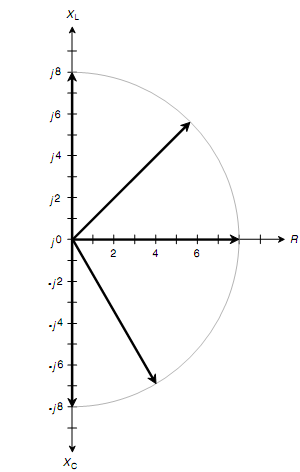
Figure: Vectors symbolizing an absolute-value impedance of 8 ohms.