Back-Face Detection Method Naming Directions:

Now the outward normal of the four faces, found by taking the cross product of any two adjacent edges of each polygon are found to be as follows :

N _PQR  = - 4i + 2 j + 6k

N_QSR  = 2i + 4 j + 2k

N _PRS = - 3i - j - 3k

N _PSQ  = 5i - 5 j - 5k

The sign of the coefficients of k shall determine the direction in which each normal is pointing, positive being in the positive direction of the z-axis. Actually, it is sufficient to compute only the coefficient of k as ( x₂  - x₁ ) ( y₃  - y ₁ ) - ( x₂  - x₁ ) ( y₂  - y₁ ) , and avoid calculation of the coefficients of i and j. The normal vectors are given in full only to indicate their orientations in Figure (a), with the two normals with positive k values being marked in full lines, and the two with negative k values being marked in broken lines.

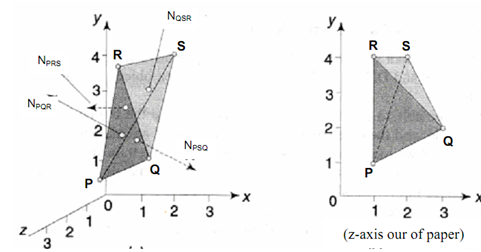
(a)                                                                 (b)

Figure: Back-Face Detection Worked Example : (a) Normals; and (b) Display

In the current case, the coefficients of k for the faces PQR and QSR are positive, and thus those two faces are visible, whereas the other two faces PRS and PSQ with negative k coefficients are hidden from view. Therefore, the display shall be as illustrated in Figure (b), with the hidden edge PS illustrated in thin broken line.