Signalling and Screening:
When we consider the consequences of asymmetric information we see the following problem: In the lemons model the problem was that sellers of high quality products did not know the quality when products of both high and low quality are marketed side by side. A solution to the problem suggested was that if sellers of a high-quality product could find some activity that was less costly for them than for sellers of a lower-quality product, then it might pay them to undertake this activity as a signal of higher quality. The buyers, too, would learn that the signal was associated with higher quality.
In the insurance example, we have discussed a form of signalling. An individual with low risk is more willing to coinsure than an individual with a high risk. Thus, the level of coinsurance was used as a potential signal of risk level. Another application considered was in education. Since education increases productivity it can act as a signal of high productivity if workers with high productivity can acquire it at a lower cost than workers with low productivity.
Consider two kinds of workers, H and P , with high productivity PH and low productivity PL. Assume that PH > PL. Then the average productivity of the workers can be written as
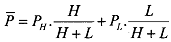
where productivity is measured in terms of the value of goods produced.
When employers cannot distinguish between workers, they may pay each worker a wage W = P. However, by acquiring a signal such as education workers with higher productivity can distinguish themselves the other category. If all high-productivity workers are educated whereas none of the low-productivity workers are, the employers will find out the high- productivity workers and pay them a wage WH = pH. On the other hand, the low-productivity workers are paid a wage WL = PL. Thus, there will equilibrium in the market.
We now look for the condition under which it can take place. Suppose that the costs of education are CH for the high-productivity workers and CL, for the low-productivity workers. In that case, we must have CH < CL and CL > PH - PL to ensure that it is not worthwhile for the low-productivity worker to invest in education. Moreover let us take CL < PH - PL so that it is worthwhile for the high productivity worker to invest in education. Thus, when education is used as a signal, those with education get a wage WH = PL and those with no education get a wage WL = PL. Finally, we must have the condition that
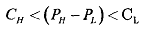
We have in a simplified way described above an equilibrium, which is called a separating equilibrium. In that the two- group of workers separate themselves by getting or not getting education. However, there are other equilibria also. Suppose that CL > PH - PL in which the low-productivity workers do not find it worthwhile to invest in education. Since every worker gets a wage P if no one gets educated and there is no separation, if CL > PH - PL then it would not be worthwhile for the high-productivity workers to get educated either. Consequently, there will be equilibrium with no one getting educated. Therefore, multiple equilibria are possible with asymmetric information.
Recall that the problem of adverse selection arises from the fact that the principal has less information than the agent about the risk involved. We have seen two examples of this. Akerlof s model of the market for lemons is discussed to highlight the problems created. When buyers are uncertain about the quality of used cars and offer to pay only a price for average quality, the better quality cars disappear from the market. This is due to the fact that the sellers of these cars do not get a fair price. In the second example, an insurance company is uncertain about the risk quality of the applicants and offers an insurance premium appropriate for average risk. As a result, individuals with lower risk drop out as they consider the premium very high.Thus, the individuals with high risk get insurance.