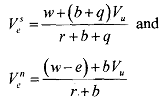Shapiro-Stiglitz Model:

Important features of the Shapiro-Stiglitz efficiency wage model  is presented in the following:

Basic Setup

Let  us  assume  that  there are N  identical, risk neutral workers. They  face an instantaneous  utility is a function of wages and effort 'normalised'  as:

u(w,  e) =  w -  e.

In  the above equation  e  is  ether  Oor  a  constant  e>  0  i.e.,  it  is  a binary variable and not continuous. The unemployed workers receive wage w ≥ 0 and the effort level e = 0. The  worker  leaves the job  with  separation rate  per  unit  time  b  that  is exogenous. Intertemporal  interestldiscount rate is taken as r . The workers objective function is

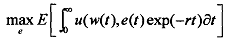
We have the workers choice at any point in time in which she decides  to exert effort or not. The odds of a worker getting caught if  shirking are  q .  If  fired, the worker  enters unemployment, waits for a new job.  The job finding rate, which will be determined in the equilibrium is a Asset Equations We consider that the value of employment is the flow value of the wage minus the capital loss of unemployment scale of its probability.

To  appreciate the  valuation  problem,  remember  that  a typical worker may transfer  from the current state of  unemployment  to  possible future state of employment. The rate at which this transfer occurs may  depend on  the individual's actions,  in two states: One  state being 'employed and working hard' and another being 'employed and taking it easy'. The model includes the following asset values:
V_u  =  Present discounted life time value of currently being unemployed
Vⁿ =  Value of currently being employed and working hard
V^s =  Value of currently being employed and shirking.

When working hard, a worker puts up effort  e and has productivity  1. When shirking, there is no effort and no productivity fiom this worker.

To find the asset value of employment, we take a short discrete time interval:

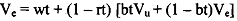
Notice we  are  for now taking V,  as given, The  wt  term gives the  flow of wages,  and the  second expression  is the discounted value of future outcome, bearing in mind that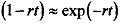

Rewriting above we get

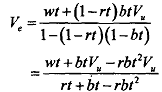
Let us move to continuous time so  that it allows t -> 0 and we write

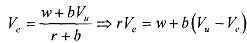
In the above  equation, notice  that value of  employment  is the flow value of the wage minus the capital loss of unemployment scaled by its probability. We  now want  to  consider  this problem separately  for  a shirker versus non- shirker:

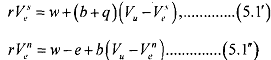
In (5.1') above,  rv  is the return to the asset vS  assuming a common interest rate  r .  The first term on the right-hand side gives the current return to wage w for a shirking worker, who does not put up any effort. The second term  is the expected value of the change  in  the asset,  (b +  q) (v_u -  vⁿ_e)  ,  where  (b +  q)  is the total rate of  change that occurs for a shirker remembering  the fact that a shirker also suffers a probability q  of being caug  and then fired).

When a worker losses her job,  V_u  - V_e^S  yields the asset change. In general, this change is negative as utility loss is associated wit losing ones  job. h  In case (5.1"). the first part of right side, i.e., we  indicates the lower current return. Why? Because  the  worker puts up effort  e  while working hard, lowering thereby  the current utility.  In  the second term,  i.e.,  b(V_u- V"_e),  the capital loss  is  suffered with smaller probability  as  q  is missing. Intuitively, this equation shows that  if  the worker  is checked now, she keeps her job  and continues receiving the return  w -  e .

we get