Subtraction of Fractions:

The common method of subtraction of fractions with general denominators is to subtract the numerators and place this difference over the common denominator.

5/8 - 2/8 = 5 ×(1/8) - 2× (1/8) = (5-2) ×(1/8) = 3×(1/8) = 3/8

While fractions do not have a common denominator, this method must be changed. For example let's consider the problem:

 1/2 + 1/3 = ?

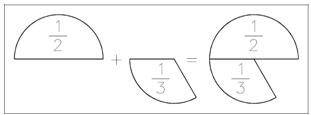
This presents a problem, the similar problem one would have if he were asked to add 6 feet to 3 yards.  In that case the entities (units) aren't equal, so the 6 feet are 1^st converted to 2 yards and then they are added to 3 yards to provide a total of 5 yards.

6 feet + 3 yards = 2 yards + 3 yards = 5 yards

Going back to the fraction addition instance, then 1/2 and 1/3 must both be expressed in the similar segments to be added.  Without developing the common method, 1/2 is 3/6ths. Multiply 1/2   by 3/3 or (one) to give the equivalent fraction.  Similarly 1/3 equals 2/6.

Then,

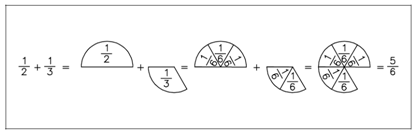
The general method of adding or subtracting fractions that do not have a common denominator is to convert the individual fractions to equivalent fractions along with a common denominator.  These evenly sized segments could then be added/subtracted.

The easiest method to compute a common denominator is to multiply the denominators.  This is acquired if each fraction is multiplied top and bottom through the denominator of the other fraction (and therefore by one, giving an equivalent fraction).

1/3 + 8/6 =

1/3 . 6/6 + 8/6 . 3/3 =

6/18 + 24/18 = 30/18

For more than two fractions, every fraction is multiplied top and bottom through each of the other denominators.  Those techniques works for simple/ small fractions. If the denominators are large or several fractions are to be added, this technique is cumbersome.