Voltage and Current Phase Relationships in an Inductive Circuit:

As previously stated, any modification in current in a coil (either a increase or a fall) causes  a corresponding change of the magnetic flux around the coil.  Because the current changes at its maximum rate whenever it is going by its zero value at 90° (point b on Figure) and 270° (point d), the flux modification is also the greatest at those times.  As a result, the self-induced EMF in the coil is at its maximum (or minimum) value at these points, as display in Figure. Since the current is not changing at the point when it is going through its peak value at 0° (point a), 180° (point c), and 360° (point e), the flux change is zero at those times.  Thus, the self- induced EMF in the coil is at its zero value at these points.

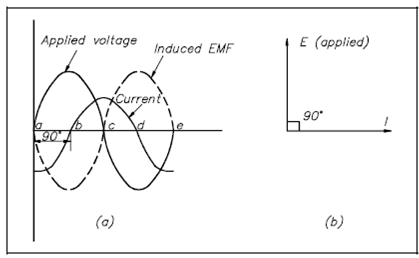
Figure: Current, Self-Induced EMF, and Applied Voltage in an Inductive Circuit

According to Lenz's Law (refer to Module 1, Basic Electrical Theory), the induced voltage always opposes the modification in current.  Referring to Figure, along with the current at its maximum negative value (point a), the induced EMF is at a falling and zero value.  Therefore, when the current rises in a positive direction (point a to point c), an induced EMF is of opposite polarity to the applied voltage and opposes the rise in current. Remember in which as the current passes by its zero value (point b) the induced voltage reaches its maximum negative value. Along With the current now at its maximum positive value (point c), an induced EMF is at a zero value and rising. Since the current is falling toward its zero value at 180° (point c to point d), the induced EMF is of the similar polarity as the current and tends to keep the current from falling.  Whenever the current reaches a zero value, the induced EMF is at its maximum positive value. Finally, when the current is increasing from zero to its maximum negative value at 360° (point d to point e), an induced voltage is of the opposite polarity as the current and tends to keep the current from increasing in the negative direction. Therefore, an induced EMF can be seen to lag the current through 90°.

The value of the self-induced EMF varies as a sine wave and lags the current through 90°, as display in Figure. The applied voltage has to be equal and opposite to the self-induced EMF at all times; thus, the current lags the applied voltage through 90° in a purely inductive circuit.

The current can be expressed as a vector that is lagging the applied voltage by 90° if the applied voltage (E) is represented through a vector rotating in a counterclockwise direction Figure.  Diagrams of these categories are referred to as phasor diagrams.