Effective Values

The output voltage of an AC generator can be expressed in two ways.  Single is graphically by use of a sine wave display in below Figure.  The second way is algebraically by the equation

e = E_max sin ωt, that will be covered later in the text.

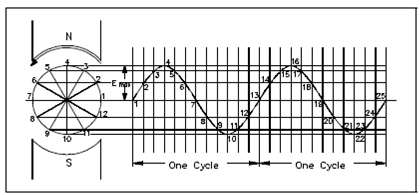
Figure: Voltage Sine Wave

Whenever a voltage is generated through an AC generator, the resulting current varies in step along with the voltage.  As the generator coil rotates 360°, the output voltage goes by one complete cycle. Within one cycle, the voltage increases from zero to E_max in one direction, decreases to zero and increases to E_max  in the opposite direction (negative E_max), and then decreases to zero again. The value of E_max occurs at 90° and is referred to as peak voltage. A time it takes for the generator to finish one cycle is known as the period or the number of cycles per second is known as the frequency (measured in hertz).

One way to refer to AC voltage or current is by peak voltage (E_p) or peak current (I_p). That is the maximum voltage or current for an AC sine wave.

Other value, the peak-to-peak value (E_p-p or I_p-p), is the magnitude of voltage, or current range, spanned through the sine wave. Therefore, the value most general used for AC is effective value. An Effective value of AC is the amount of AC which generates the similar heating effect as an equivalent amount of DC. Within easier terms, a single ampere effective value of AC will generate the similar amount of heat in a conductor, in a provided time, as one ampere of DC.  The heating effect of a given AC current is proportional to the square of the current.  Effective value of AC could be calculated through squaring all the amplitudes of the sine wave over one period, taking the average of these values, and then taking the square root.  The effective value, being the root of the mean (average) square of the currents, is called as the root-mean-square, or RMS value.  In sequence to understand the meaning of effective current applied to a sine wave that was refer to Figure.

The values of I are plotted on the upper curve, and the equivalent values of I² are plotted on the lower curve. The I² curve has double the frequency of I and varies above and below a new axis.  A new axis is the average of the I² values; the square root of that value is the RMS, or effective value, of current. An average value is ½ I_max².  The RMS value is then

√2I²_max /2 OR (√2/2) I_max, which is equivalent to 0.707 I_max.

There are six basic equations which are used to convert a value of AC voltage or current to another value, as listed down.

Average value                    = peak value x 0.637                                               

Effective value (RMS)          = peak value x 0.707                                   

Peak value                         = average value x 1.57                                

Effective value (RMS)          = average value x 1.11                    

Peak value                         = effective value (RMS) x 1.414                 

Average value                    = effective (RMS) x 0.9                                

The values of current (I) and voltage (E) which are generally encountered are supposed to be RMS values; thus, no subscript is used.

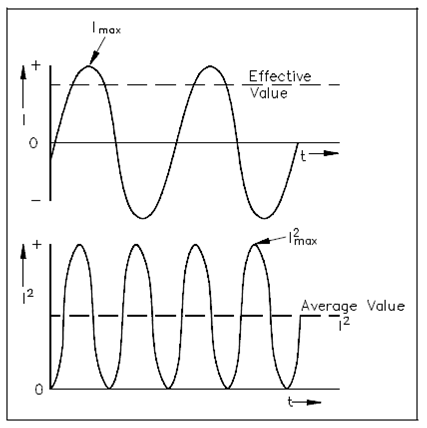
Figure: Effective value of current

Another useful value is the average value of the amplitude in during the positive half of the cycle. Within the Equation (7-7) is the mathematical relationship among I_av, I_max, and I.

I_av  =    0.637 I_max  = 0.90 I                        (7-7)

Below Equation is the mathematical relationship among E_av, E_max, and E.

E_av =   0.637 E_max =   0.90 E               (7-8)