3-Dimensional Scaling:

In 3-D, Scaling is also an extension of scaling in 2-D. Similar to the 2-D case, if S_x = S_y = S_z then object shapes are maintained, else they are deformed. S_x, S_y and S_z are the scaling factors respectively in x, y and z directions.

Scaling x′ = x * S_x

            y′ = y * S_y

            z′ = z * Sz

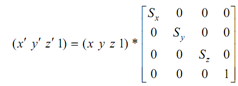
Entire scaling may be obtained by utilizing the fourth diagonal element, that means

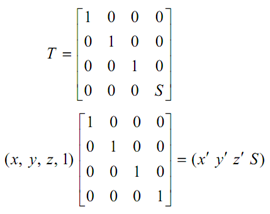
It is obvious that in this case

 (x* y*  z* 1) = (x′ /s, y′/s, (z′ /s) 1).

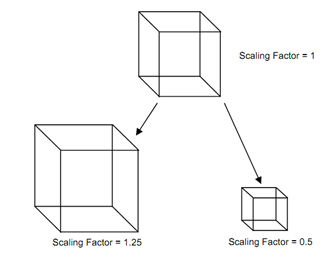
Figure: 3-Dimensional Scaling

If object is not centred at the origin (0, 0, 0) scaling transformation causes size alter and movement of the object both. Though, scaling around a fixed point

P₀ (x₁ y₁ z₁) may be accomplished by

1.      translating P₀ to the origin

2.      scale the object

3.      translating P₀ back to original position.

So the composite matrix is T = (- x₁ , - y₁ , - z₁ ) ∗ S (S _x , S _y , S _z ) * T ( x₁ , y₁ , z₁ ) .

For inverse scaling replace S_x with 1/ S _x , S_y with 1/ S _y , and S_z with 1/S _z , then S (S ^-1 ) = 1