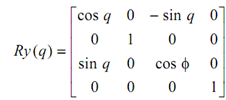Rotation about z, x and y-Axis:

Z-axis rotation is alike to the 2-D case:

In this, coordinates against z-axis are kept constant.

 x′ = x * cos φ - y * sin φ

 y′ = x * sin φ + y * cos φ

  z′ = z

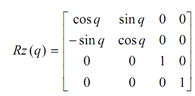
Rotation around x-axis is same as rotation around z-axis.

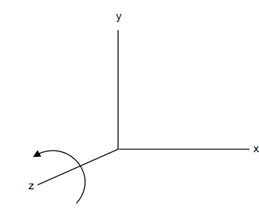
Figure: Rotation about z-axis

If x-axis, y-axis & z-axis are replaced through y, z and x-axes respectively

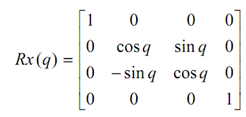
So we do the similar replacement in the equations:

y′ = y* cos q - z * sin q

 z′ = y* sin q + z* cos q

 x′ = x

Likewise, rotation about y-axis is same as rotation around z-axis if x, y and z-axes are replaced by z, x and y-axes respectively.

Figure: Rotation about y-axis

So we do the same replacement in equations :

z′ = z* cos q - x* sin q

x′ = z* sin q + x* cos q

 y′ = y