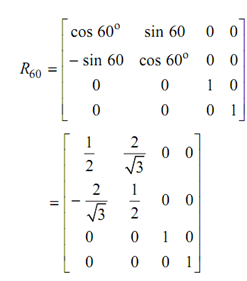Determine transformation:

The pyramid described by the coordinates A (0, 0, 0), B (2, 0, 0), C (0, 2, 0) and D (0, 0, 2) is rotated by 60^o about a line L that has the direction V = J + K and passing through point C (0, 2, 0).

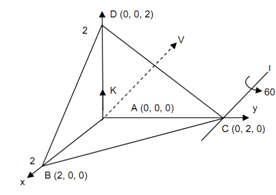
Figure

Solution

The rotation matrix R_{θ, L} may be found by concatenating the matrices. The required transformation may be obtained by following the under stated steps:

1.      Translate point C to the origin.

2.      Align V with the vector K.

3.      Rotate by θ^o about K.

4.      Reverse steps (2) and (1).

So the rotation matrix R_{θ, L} is

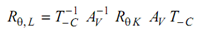
Along with C = (0, 2, 0) then

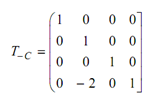
To determine transformation AV which align vector V with the vector K along the positive z-axis.

Figure

Vector V may be aligned with the vector through the following sequence of transformation.

Rotate around x-axis by an Angle θ₁ (Vector V₁)

From above Figure

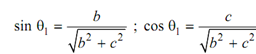
So the needed rotation about x-axis.

Applying the rotation to vector V generates vector

As V = J + K   ∴ a = 0, b = 1 and c = 1.

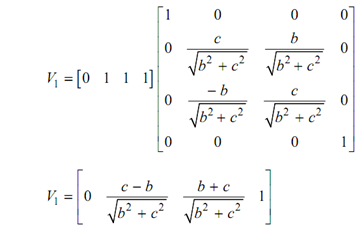
Coordinates of the rotated figure may be found by applying R_{θ, L} to the matrix of homogeneous coordinates of vertices A, B, C and D.

?  ?

∴  We can find R_{θ L} . C .