y-shear about the origin - 2-d and 3-d transformations
Suppose an object point P(x,y) be moved to P'(x',y') in the x-direction, through the specified scale parameter 'b'. that is, P'(x'y') be the result of y-shear of point P(x,y) through scale factor 'b' regarding the origin, that is demonstrated in Figure 5(a).
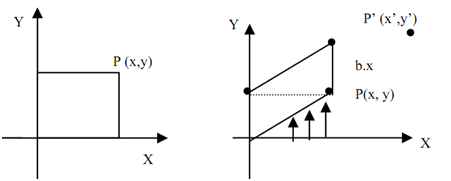
Figure: 5(a)
Hence, the points P(x,y) and P'(x',y') have the subsequent relationship :
|
x' = x
|
|
|
y' = y+bx
|
= Shy(b)
|
Here 'b' is a constant (termed as shear parameter) which measures the degree of shearing. In matrix form, we contain:
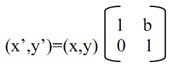
In terms of Homogeneous Coordinates, above equation (16) is:
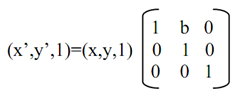
There is, P'h = Ph.Shy(b)
Here Ph and P'h represents object points, before and after needed transformation, in Homogeneous Coordinates and Shy(b) is termed as homogeneous transformation matrix for y-shear along with scale factor 'b' in the y-direction.