X-shear Regarding the Origin - 2-d and 3-d transformations

Suppose an object point P(x,y) be moved to P'(x',y') in the x-direction, via the given scale parameter 'a',that is, P'(x'y') be the outcome of x-shear of point P(x,y) through scale factor a regarding the origin, that is demonstrated in Figure 4.

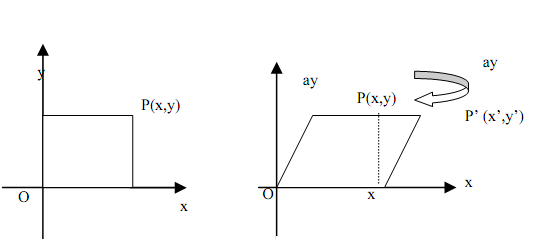
Hence, the points P(x,y) and P'(x',y') have the subsequent relationship:

x' = x + ay

y' = y         

= Sh_x(a)                                                    ------(11a)

Here 'a' is a constant (termed as shear parameter) which measures the degree of shearing.  The shearing is in the opposite direction, if a is negative.

Remember that P(0,H) is taken into P'(aH,H).  This obeys that the shearing angle A which is the angle by that the vertical edge was sheared; is specified by:

tan(A) = aH/H = a.

Consequently the parameter a is simply the tan of the shearing angle. Within matrix form of 2-D Euclidean system, we contain:

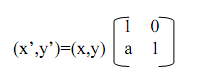
(12)

In terms of Homogeneous Coordinates, above equation (12) is:

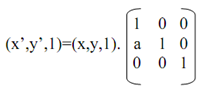
-----------------------(13)

That is, P'_h = P_h Sh_x(a)   --(14)

Here P_h and P'_h represent object points, before and after needed transformation, in Homogeneous Coordinates and Sh_x(a) is termed as homogeneous transformation matrix for x-shear along with scale parameter 'a' in the x-direction.