Write Some Notes for the Gauss-Seidel Method?
1. Equation below is used to calculate the voltage at each busbar in turn, always using the most up to date values for the other busbar voltages. For most systems, the voltages will gradually converge although there are ill conditioned systems in which this convergence fails.
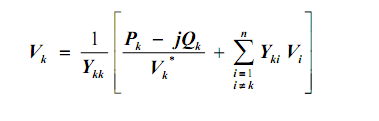
2. When using above equation, remember that (Pk - j Qk) is the power flowing into node k (generation). For power flowing out of the node (loads), it is represented by negative power [i.e. - (Pk - j Qk)].
3. In the calculation, successively more accurate values of busbar voltage are found. At some stage it is necessary to stop the iterative process as sufficient accuracy has been secured. One may chose to stop the process when no bus voltage changes by more than 0.1% in per unit terms. The calculated voltages are then applied to the network to work out the active and reactive power powers at all busbars.
4. The Gauss-Seidel method is at times slow to converge and an acceleration factor can often be usefully applied. The change to the bus voltage in complex form is calculated and then multiplied by an acceleration factor before the new bus voltage value is calculated. The acceleration factor may range up to 2 and is largely a function of the network. A value of 1.6 is widely used. If a value less than 1.0 is chosen, this may help an otherwise divergent system to converge.
5. In order to apply the method one of the generator busbars must be specified as having a fixed voltage with the power unknown. This is referred to as the reference or slack busbar and takes up power which is equal to the difference between the specified generation and the sum of the loads plus losses.
6. At any busbar, the active power (P) and reactive power (Q) may be specified and the voltage magnitude and angle are calculated. Such busbar is termed a PQ busbar. If the active power and voltage magnitude are specified, the reactive power and voltage angle are calculated. Such a busbar is known as a PV busbar and is appropriate for generation busbar.
7. The Gauss-Seidel method is simple in approach, however, other methods that offer certain advantages are available such as the Newton-Raphson method and the fast decoupled load flow. The latter is almost an industry standard.