You should use the BToolkit to produce the answers to the questions below. Where applicable, please use the machine names and identifier names suggested in the question to help me find and mark your answers. Obviously, you can choose names for additional machines etc as required. I suggest you make a single directory for your work for this assignment (eg, ass1dir ). When you are ready to submit, go to the directory above ass1dir and create a tar file with all your work in:

tar -cvf ass1dir.tar ass1dir

then gzip it:

gzip ass1dir.tar ass1dir.tar.gz

You should generate proof conditions at each stage and examine them in the prover.

You are not required to prove all the conditions, but you should examine the ones that don't auto prove to check that they are true. Otherwise, modify your machine. All machines should have invariants which are strong enough to prove machine consistency. You should provide comments within your machines to explain what they are doing, detail any design decisions made, any problems encountered etc. If different approaches or interpretations are possible, comment your machine to explain what you have done and why. Additional comments (for example, justification for any unproved conditions for that machine) are welcome.

Question 1

Write an implementation for the Prime machine (defined at the end of the assignment sheet). Provide a suitable invariant and variant for any loop you use. Provide comments in your machine stating the precondition and post condition which the initialised loop meets.

Question 2

An abstract machine, Buffer is defined at the end of this assignment sheet. Provide a refinement of this machine which stores the queue in an array:

aa : 1 . . qlen → ELEM

When elements are removed from the front of the queue, the array itself is not altered but the positions become available for overwriting. When adding elements, once the end of aa is reached, wrap-around can occur if positions at the front of aa are available. Thus for example, if the capacity is 8, the sequence [a, b, c, d] may correspond to:

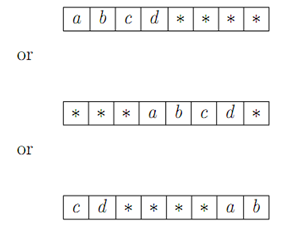
etc (where * indicates any element).

To do this you will need to introduce some further state variables to keep track of the situation in the array and to enable you to relate the state of aa to the state of buff. Provide the linking invariant which captures this invariant and incorporate it in a refinement machine BufferR.

In this question, getting the linking invariant right is tricky.