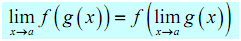"Working" definition of continuity

A function is continuous in an interval if we can draw the graph from beginning point to finish point without ever once picking up our pencil. The graph has just two discontinuities as there are only two places where we ought to be picked up our pencil in sketching it.

In other terms, a function is continuous if its graph contains no holes or breaks in it.

For several functions it's simple to find out where it won't be continuous.  Functions won't be continuous where we contain things such as division by zero or logarithms of zero.  Let's take a rapid look at an instance of determining where a function is not continuous.

Example   Find out where the function below is not continuous.

                            h (t ) =4t + 10 / t ² - 2t -15

Solution

Rational functions are continuous everywhere apart from where we have division by zero.  Thus all that we have to determine where the denominator is zero. That's simple enough to find out by setting the denominator equivalent to zero & solving.

                                        t ² - 2t -15 = (t - 5) (t + 3) = 0

Thus, the function will not be continuous at t=-3 & t=5.

A nice consequence of continuity is the given fact.

Fact 2

If  f ( x ) is continuous at x = b and 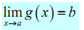then,