The following exercises may help you to look more closely at the activities done above.

E1) Why did the two dice game become more difficult?

E2) Do you find the activities in Example 4 helpful as a means of understanding ones, tens and their relationship? If so, in what way? If not, write down an activity, different from the ones given in this unit so far, which would help children understand ones/ tens/hundreds.

What is the underlying principle involved in the activities given in Example 4? Is it not the principle of exchange ? That is, the principle that 'one of these is ten of those', and so on, as we move leftwards from one place to the next in a numeral ? As you have seen, a child needs to thoroughly understand this principle to be able to handle the four arithmetic operations, correctly and easily. In fact, we can gauge whether a child has understood the idea by the ease with which she can handle the hundreds/ tens/ones in the following cases of mental arithmetic.

i) Mentally adding 1, 10 or I00 (or its multiples) to any given number, especially examples containing the digit 9 (for example, 93 + 10).

ii) Mentally subtracting 1, 10 or 100 (or its multiples) from any given number, especially examples containing the digit 0 (for example, 804 -10).

Here, is an example of a mental activity which might help children to get used to mental addition or subtraction. This activity can be done by a large number of children, divided into 3 or 4 groups, or by a single child.

On a blackboard write headings like the following:

SUBTRACT I    ADD 2     SUBTRACT 100     ADD 20

Then, below each of them one can write down some numerals, and ask the different groups of children to continue the rest of the column. For example, you could write 404, 184, 90 I, and 150 below each of the above headings. Then the groups can give you the answers to 404 - 1, 184 + 2, 90 1 - 100, 150 + 20. The group that answers correctly first can get a-point. The game can continue in this way.

Similarly, if the children are working individually, you can give each child a worksheet with these kinds of headings. They could be asked to fill 8 steps, say, in each column in the sheet in a stipulated time, by performing mental operations. So, for example, if the column headed 'Subtract 100' starts with 801, a child would finish up writing : 801, 701, 601, 501 ,...... 1..

This activity can be adapted to any situating we want. For instance, with

I 1-year-olds, or older children, the worksheet can be

SUBTRACT l paise .          ADD 2p.                 SUBTRACT Re1 /-                ADD 20p. ,

Rs. 404                                 Rs. 184                              Its 9.01                                Rs. 1.50

Another, more interesting, form of the activity for 9 or 10-year-olds can be using the grid in Fig. 6 (a). The instruction for moving across and down the grid can be any combination of ADD 1, SUBTRACT 1, ADD 10, SUBTRACT 10, ADD 100, SUBTRACT 5, and so on. A starting numeral is written in the top left corner and a finishing numeral in the bottom right corner.

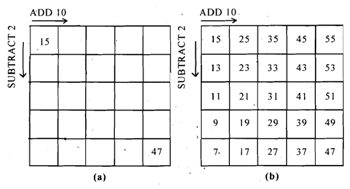
Children can work individually in completing these grids, ensuring that they obey the given instruction for all movements left to right along the rows or down the columns.